Urban travel carbon emission mitigation approach using deep reinforcement learning – Scientific Reports

Case selection: Ningbo City

This study focuses on the central urban area of Ningbo as a case to explore strategies for mitigating travel carbon emissions through the optimization of small-scale land use configuration. By employing this design approach and AI framework, the research aims to provide insights and references for other cities undergoing similar transitions toward green and low-carbon development.

Ningbo City, covering approximately 98.64 km², is located in the eastern coastal region of Zhejiang Province. Historically an important port city, Ningbo has evolved into a major economic hub within the Yangtze River Delta due to its advantageous land and sea transportation conditions. In 2022, Ningbo implemented the “New Era Beautiful Ningbo Construction Plan”, with the goal of developing a sustainable city by 2035, integrating spatial, economic, environmental, urban–rural, and cultural dimensions, as well as enhancing port city functionalities and institutional frameworks.

Under this plan, the central urban area of Ningbo faces unprecedented opportunities and challenges. It must balance high-quality economic development with the optimization and protection of the ecological environment, exploring innovative pathways for green manufacturing and a low-carbon economy. Additionally, as a pilot and demonstration zone for policy implementation, Ningbo’s central urban area needs to achieve coordinated development across the economy, society, and environment through improved urban management and infrastructure. Based on this urgent need, the researchers selected Ningbo’s central urban area as the study area to mitigate travel carbon emission, covering the geographical range between 121.425575 to 121.585575 longitude and 29.770178 to 29.930178 latitude (see Fig. 1).

Urban features

In AI research, urban features are abstracted into feature vectors representing various attributes and metrics of different urban areas. These feature vectors can include information on population density, land use types, public facilities distribution, transportation networks, and environmental quality. By numerically and vectorizing urban features, AI models can more efficiently analyze and process complex urban data, providing scientific decision support for urban planning and management.

Data collection

To study the impact of different urban functional configurations on carbon emissions, researchers obtained point of interests (POI) data from Amap.com to represent urban functional configurations. The categories include residential areas, companies/enterprises, science and education, dining, shopping, scenic spots, train stations, airports, and healthcare.

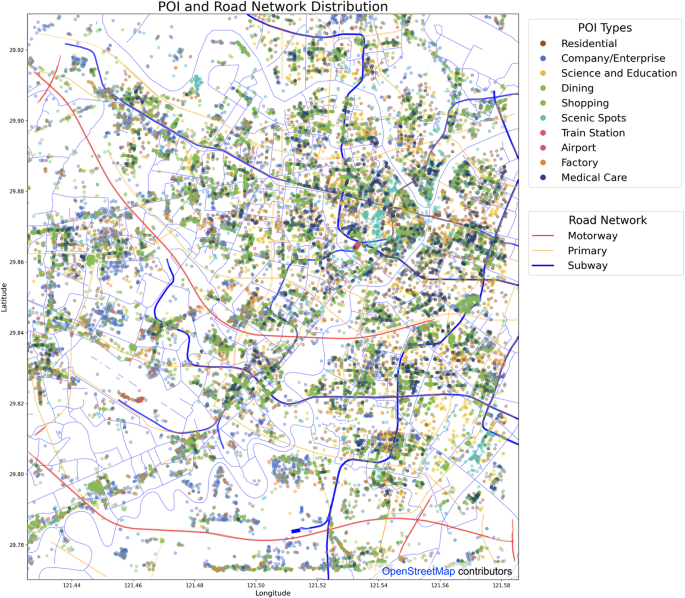
Road data was collected from OpenStreetMap (OSM), focusing on motorways, primary roads, and subways. Motorways and primary roads were used to represent the road structure for vehicle travel calculations, while subway data represented the distribution of public transportation. Both types of data influence travel preferences and mode choices. The distributions are shown in Fig. 2.

Distribution map of POI and road structure data. (The figure was created by authors, using Python and PyCharm).

All relevant data used in this study were obtained via API interfaces from Amap.com and OpenStreetMap.org, adhering to their respective terms of service and licenses. The data was used solely for personal, non-commercial academic research.

The study area is divided into an M × N matrix, with each cell represented by a d-dimensional feature vector. Therefore, the 3D tensor X represents the entire urban matrix, as shown in Eq. (1):

where X_ij represents the k-th feature of cell (i,j).

Data analysis and process

The POI data within this area was statistically analyzed and categorized as shown in the Table 1.

These POI data were mapped into 0.01° × 0.01° matrix cells based on their latitude and longitude coordinates, and the number of each POI type within each cell was calculated. This matrix representation of POI data effectively reflects the distribution of various urban functions within each cell. Additionally, the three-layer transportation network was mapped onto the matrix cells accordingly. To better understand the distribution of different land use types across the city, heatmaps were generated for various POI categories, as shown in Fig. 3.

Heatmaps showing the distribution of various POI types. (The figure was created by authors, using Python and PyCharm).

The current heatmap reveals that the residential areas in the central region of Ningbo are relatively concentrated, forming a polycentric pattern with one primary center and two secondary centers. The core of Ningbo’s old town lies slightly east of the center of the test area, while the southeastern area represents the core of the new town (Yinzhou District). The western secondary center is a recently developed area. The distribution of education, healthcare, dining, and shopping facilities is similar to that of residential areas. Companies and enterprises are distributed relatively evenly, without significant spatial differentiation. Factories, on the other hand, show considerable differences, with a much higher density in the western region compared to the eastern region. As Ningbo is a port and manufacturing city, this suggests that a large number of factory workers may need to commute long distances.

The road system data were extracted separately and matrixed. Cells intersected by different types of roads were marked as 1, 2, or 3, corresponding to motorways, primary roads, and subway lines, respectively. Figure 4 shows the road system distribution and the accessibility heatmap for each cell based on this matrix representation. These road-labeled city matrices form the basis for the subsequent Discrete Choice Models (DCM), which calculate the probability of choosing different transportation modes.

Heat-maps of transportation distribution and accessibility. (The figure was created by authors, using Python and PyCharm).

The accessibility heatmap reveals that, for the western factory area, transportation mainly relies on lower-tier roads (not shown in the figures), while public transportation is concentrated in the traditional residential centers and the new town area in the southeast. Residents in the western secondary center lack fast and convenient public transportation options (except for buses).

Methodology and technical framework

This research comprises two main components. The first involves constructing a mapping relationship between building types or land use functions and carbon emissions, including data collection, processing, and carbon emission calculations. The second part entails design and training of the deep reinforcement learning model and algorithm, where the agent determines action strategies through actions, rewards, and environmental states. The technical framework is demonstrated in Fig. 5.

Methodology and technical framework. (The figure was created by authors).

Environment design

The environment provides the urban model in which the agent operates. In a reinforcement learning framework, the agent observes the state of the environment, executes actions according to a certain policy, and receives rewards or penalties from the environment. This feedback helps the agent learn how to improve its behavior to maximize long-term returns. The environment uses urban data to establish corresponding carbon emission maps, forming the basis for rewarding reinforcement learning agent behavior.

To reflect the purpose of this study, which is the impact of building type configuration on urban transportation carbon emissions in a small urban area, researchers chose to use a discrete choice model for carbon emission estimation. Discrete Choice Models (DCM) are statistical models used to analyze and predict individual choice behavior among a finite set of discrete options. Travel choices and corresponding commuting carbon emissions are influenced by the number of 8 types of POIs in each cell of the matrix and the distribution of the transportation system. The functional expression is as Eq. (2):

where E_ij is the carbon emission of cell (i,j). Q_ij is the travel intensity of cell (i,j). Distance_ij is the distance from cell (i,j) to cell (k,l). P_ijt is the probability of choosing transportation mode t. E_t is the carbon emission coefficient of transportation mode t.

Travel intensity Q_ij can be defined as the sum of the residential POI quantity in cell (i,j) multiplied by the quantity of other POIs in cell (k,l), as shown in Eq. (3):

where N_ij^Residential is the quantity of residential POIs in cell (i,j), and N_kl(p) is the quantity of the pth type of POI in cell (k,l).

The probability of choosing transportation mode Pijt is calculated using a Logit model, as shown in Eq. (4):

where U_ijt is the utility function of choosing transportation mode t from cell (i,j) to cell (k,l), as shown in Eq. (5):

β₀: Base utility of the transportation mode, indicating the basic attractiveness of a transportation mode without other influencing factors (e.g., distance and connection type).

β₁: Coefficient of the effect of distance on utility. Typically, the farther the distance, the lower the utility of the transportation mode, so the distance coefficient is usually negative.

β₂: Coefficient of the effect of connection type on utility. For example, if a route has a subway connection, the utility of public transportation increases, so the coefficient of subway connection should be positive.

β₃: Coefficient of the effect of the nearest distance to a public transportation line, applicable only to public transportation.

Based on experience, we set four groups of β values as follows:

β_walk = [1, − 0.1,0].

β_bike = [0.5, − 0.1,0].

β_{public_transport} = [1,0.5,1, − 0.05].

β_car = [2,0.5,0.5].

These four sets of β values determine the propensity to choose different modes of transportation under various urban conditions, such as public transportation and road structure distribution. Since this study focuses more on the framework, detailed parameter adjustments will be explored in future research.

Carbon emissions of the environment are calculated using the discrete choice model, and the calculation logic is shown as Table 2.

State space

State space is crucial for the agent to make decisions and evaluate its long-term benefits. The design of the state space directly determines the convergence ability, convergence speed, and final performance of the DRL algorithm. In urban areas, converting information of each plot into a state may result in an excessively large state space. To make the state space more compact, the urban space is gridded, and each cell’s state features describe the area. The state space of each cell can be represented by an 8-dimensional vector, representing the quantity of 8 functional POIs, considering the special role of transportation facilities in urban design. These 8 functions are residential, companies, science and education, dining, shopping, scenic spots, and healthcare. Therefore, the state space S can be defined as Eq. (6):

where M and N are the dimensions of the test area matrix, and each state, s ∈ S, is a 3D tensor of size M × N × 8. The state of each cell (i,j) is represented by an 8-dimensional vector, as shown in Eq. (7) :

where x_i,j,k represents the quantity of the kth functional POI in cell (i,j).

Action space

Each action generated by the agent corresponds to an environmental feature. This action specifies the quantity of different types of POIs at a specific location in the environment. The action is also an 8-dimensional vector, describing the adjustment of the quantity of POIs corresponding to residential areas, companies and enterprises, daily services, dining, shopping, parks and green spaces, industrial parks, and medical facilities. Therefore, the action space is divided into two parts: selecting the cell to be modified (i,j), and modifying the state vector of the cell Δs_i,j. The action space is as shown in Eq. (8):

The process of selecting cells uses a mixed strategy, based on an exploration–exploitation balance. In the greedy algorithm, the agent always selects the action with the highest estimated value. When the agent decides to exploit, it selects the cell with the highest value, show as Eq. (9):

where v_k is the state value calculated by the critic network, and S_flatten is the flattened state matrix S, as shown in Eqs. (10) and (11):

In the exploration strategy, the agent selects random actions with a certain probability to explore new states and possible strategies, with the probability of exploration gradually decreasing during training, as shown in Eq. (12):

where ξ is a random number uniformly distributed between 0 and 1.

To prevent issues such as gradient explosion, the agent’s actions cannot significantly change the quantity of a particular type (k) POI in a single cell (i,j). Therefore, the action Δs_i,j,k modifies its state with three rules, including multiplicative update, additive update, and value constraint.

Multiplicative update: For non-zero state components, use multiplicative update, as shown in Eq. (13):

Additive update: For zero state components, use additive update, as shown in Eq. (14):

Value constraint: Ensure all state components are non-negative integers, as shown in Eq. (15):

Therefore, for a given current state s_i,j,k and action Δs_i,j,k the updated state s′_i,j,k is calculated as Eq. (16):

This state update method combines additive and multiplicative update mechanisms to accommodate different state component values and ensure that the updated state components remain within the non-negative integer range. Additionally, this mechanism ensures that within a limited number of steps per round, the agent cannot take shortcuts by setting all POIs of a particular cell to zero. Instead, the agent must choose the cells with the highest optimization value for action, even if it wishes to reduce or eliminate a specific POI in a cell.

Termination conditions

Setting appropriate termination conditions in the reinforcement learning environment is crucial for controlling the training process and ensuring convergence. In this study, we simply set success and failure conditions:

• Success: If the current carbon emissions have decreased by a certain percentage θ (e.g., 5%) compared to the initial carbon emissions, the task is considered complete.

• Failure: If the agent’s action steps t exceed the predetermined maximum steps T_max, the task is terminated.

Therefore, the specific termination condition logic is as Eq. (17):